Searching algorithms help locate elements in a data structure efficiently. Two fundamental searching techniques are Linear Search and Binary Search. These algorithms form the basis of many advanced searching techniques used in computing.
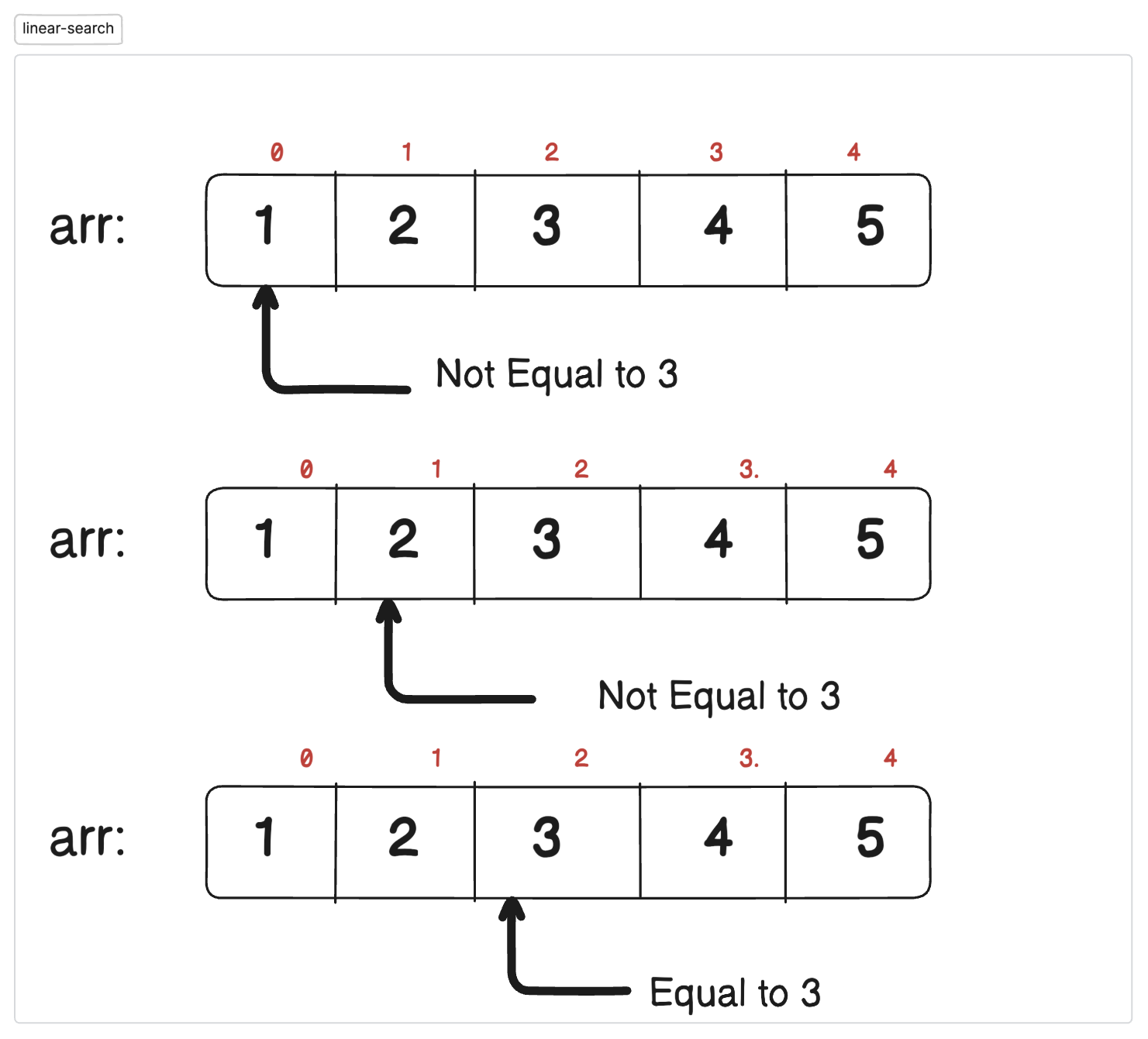
Linear Search is a simple search technique that sequentially checks each element in the array until the target element is found or the list ends.
Start from the first element.
Compare the target element with the current element.
If they match, return the index.
If not, move to the next element.
Repeat until the element is found or the list is exhausted.
Best case: O(1) (Element is found at the beginning)
Worst case: O(n) (Element is at the end or not present)
Average case: O(n)
#include <iostream>
using namespace std;
void linear_search(int arr[], int target){
for(int i=1; i<=9; i++){
if(arr[i-1]==target){
cout<<"Element Found at "<<i-1<<"th index";
return;
}
}
cout<<"Element Not Found";
return;
}
int main()
{
int arr[9]={1,2,3,4,5};
int target = 3;
//Linear Search to find target
linear_search(arr, target);
return 0;
}
Simple and easy to implement.
Works on both sorted and unsorted data.
Inefficient for large datasets.
Time complexity is linear, making it slow compared to other searching techniques.
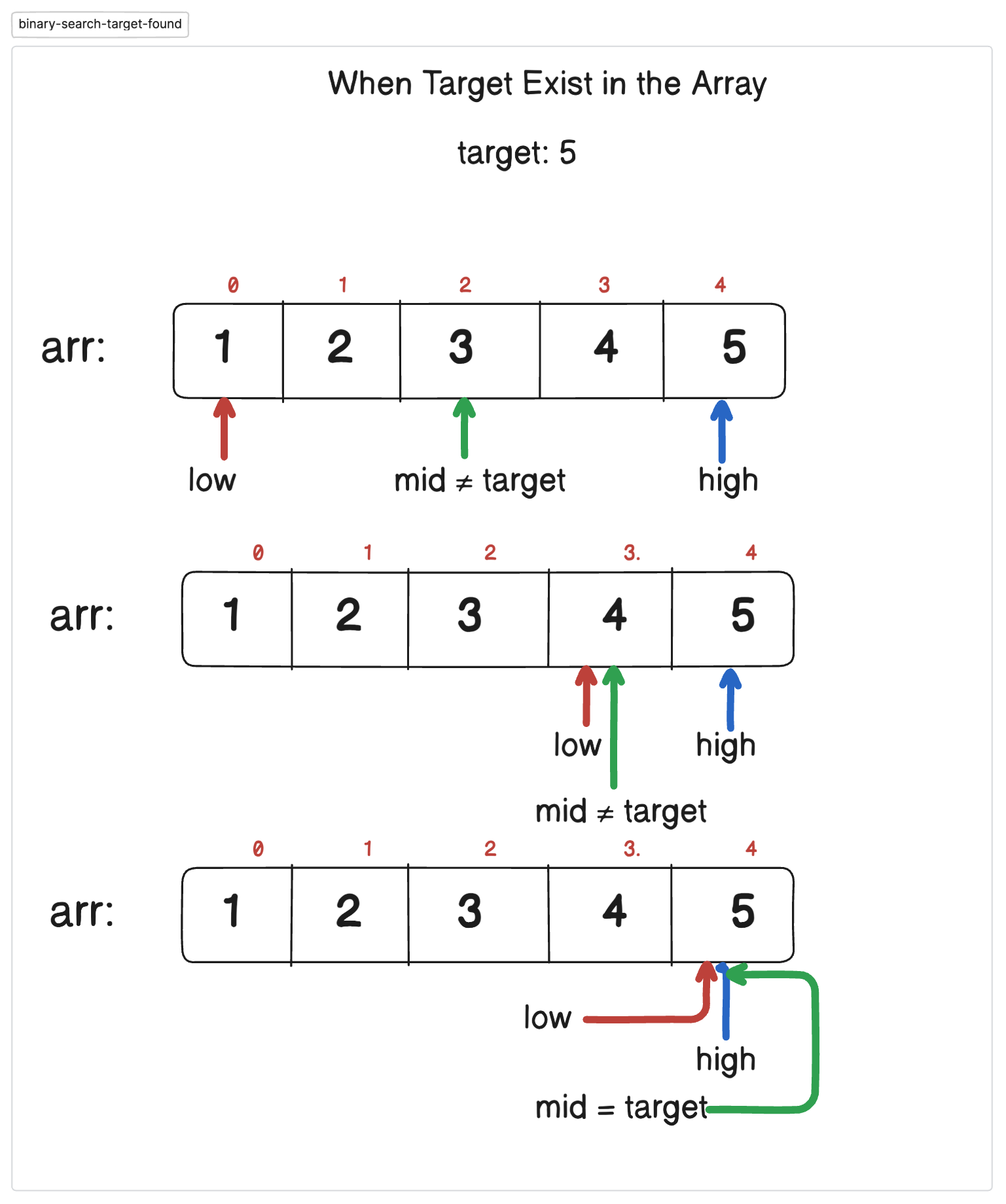
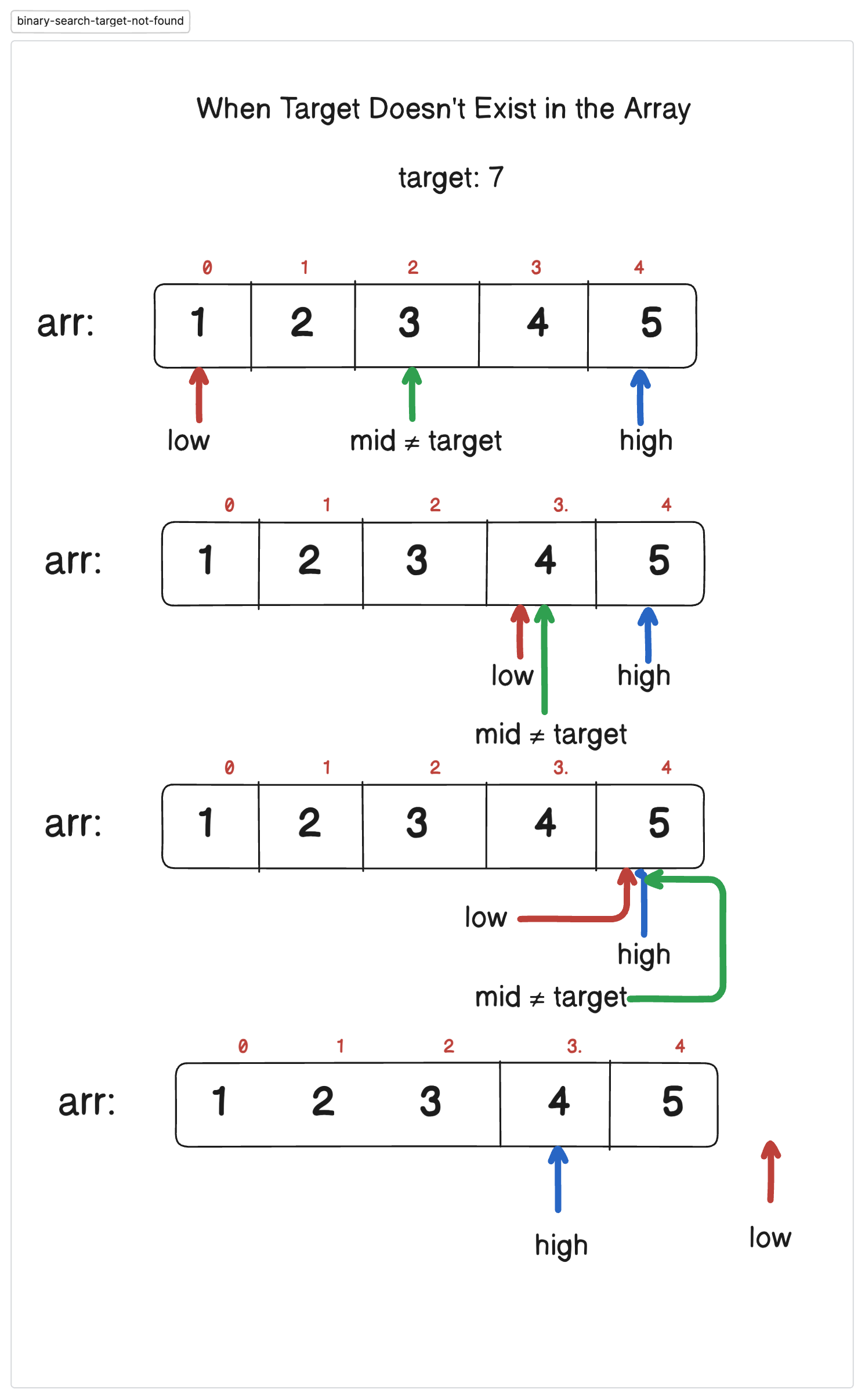
Binary Search is an efficient searching technique that works on sorted arrays by repeatedly dividing the search space in half.
Set two pointers: low (start of array) and high (end of array).
Find the middle element.
If the middle element matches the target, return its index.
If the target is smaller, search the left half; otherwise, search the right half.
Repeat until the element is found or the search space is empty.
Best case: O(1) (Element found at the middle)
Worst case: O(log n)
Average case: O(log n)
#include <iostream>
using namespace std;
void binary_search(int arr[], int size, int target){
int low=0, high=size-1;
while(low<=high){
int mid = (low + high) / 2;
if (arr[mid] == target) {
cout << "Element found at index: " << mid ;
return;
}
else if (arr[mid] < target) {
low = mid + 1;
}
else {
high = mid - 1;
}
}
cout << "Element Not Found" << endl;
}
int main()
{
int arr[9] = {1,2,3,4,5};
int size = sizeof(arr) / sizeof(arr[0]);
int target = 5;
// Binary Search to find target
binary_search(arr, size, target);
return 0;
}
More efficient than Linear Search, especially for large datasets.
Has a logarithmic time complexity.
Works only on sorted data.
Requires additional sorting if the data is unsorted, which increases preprocessing time.
Both Linear Search and Binary Search have their own use cases:
Linear Search is useful for small or unsorted datasets.
Binary Search is ideal for large datasets that are already sorted.
Choosing the right search algorithm depends on the nature of the data and the performance requirements of the application.
Get the latest coding tips, industry trends, and exclusive learning resources delivered straight to your inbox. Subscribe now and never miss an update!